Atomic physics provides a framework for understanding the unique properties of elements, including potassium. The Bohr model, a foundational concept in quantum mechanics developed by Niels Bohr, offers a simplified yet insightful representation of atomic structure and electron behavior. Spectroscopy, a technique extensively used in analytical chemistry laboratories, allows for the precise measurement of emitted light wavelengths. The interaction between these concepts manifests clearly in potassium’s emission spectrum and its bohr model showing the electron transitions, revealing quantized energy levels. Analyzing this spectrum, a core skill in materials science research, allows scientists to validate the predictions of the Bohr model and gain a deeper understanding of the electronic structure of potassium. These transitions, specifically, demonstrate the principles of quantum mechanics at the atomic level.
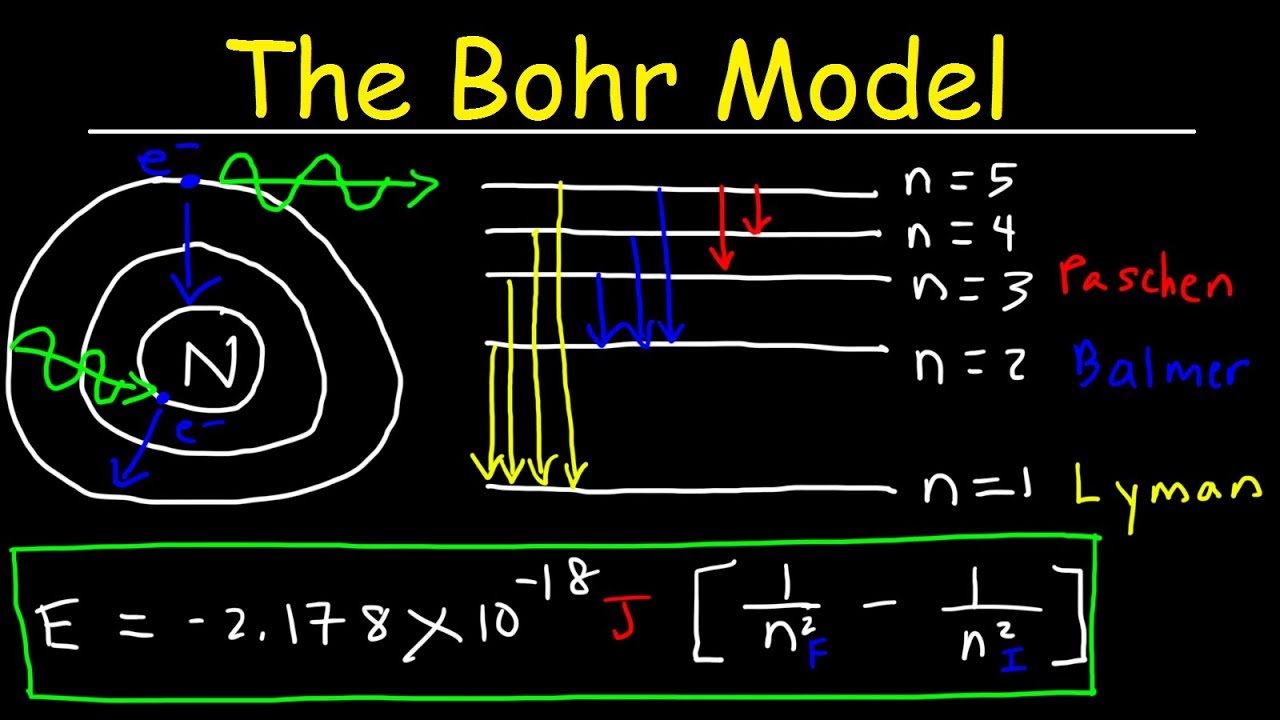
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Bohr Model of the Hydrogen Atom, Electron Transitions, Atomic Energy Levels, Lyman & Balmer Series .
Potassium (K), an alkali metal nestled in Group 1 of the periodic table, is far more than just an entry in chemistry textbooks. It’s a crucial element with a pivotal role spanning diverse domains – from sustaining life through nerve function and muscle contraction in living organisms, to enriching agricultural practices as a key component of fertilizers, and even influencing industrial processes. Its pervasive presence underscores the importance of understanding its fundamental properties.
One of the most revealing ways to understand potassium is through its emission spectrum.
Defining the Emission Spectrum
An emission spectrum is essentially the "fingerprint" of an element. It’s the unique pattern of light wavelengths emitted by an element when its atoms are excited. This excitation typically occurs when the element is heated or subjected to an electrical discharge.
When atoms are excited, their electrons jump to higher energy levels. Upon returning to their original, stable energy levels, they release energy in the form of photons – packets of light.
The wavelengths (and thus colors) of these photons are specific to the energy level transitions within the atom.
Because each element possesses a unique atomic structure and set of energy levels, its emission spectrum is correspondingly unique.
This uniqueness is what makes emission spectroscopy a powerful tool for qualitative analysis, enabling scientists to identify the elemental composition of a sample, no matter how complex.
Purpose of this Article: Potassium and the Bohr Model
This article aims to dissect the emission spectrum of potassium through the lens of the Bohr model, a foundational concept in atomic physics.
We will delve into the electron transitions within the potassium atom that give rise to its characteristic spectral lines.
By applying the principles of the Bohr model, we can gain a simplified yet illuminating understanding of how the quantized nature of electron energy levels dictates the specific wavelengths of light emitted by potassium.
This exploration will highlight the power of the Bohr model in explaining atomic phenomena, while also acknowledging its limitations in the face of more complex quantum mechanical descriptions.
The Bohr Model: A Stepping Stone to Understanding Atomic Emission
Before delving into the specifics of potassium’s spectral signature, it’s essential to revisit the Bohr model of the atom. While superseded by more sophisticated quantum mechanical models, the Bohr model provides an intuitive and accessible framework for understanding atomic emission, particularly when considering elements with simpler electronic structures.
A Brief Overview of the Bohr Model
Proposed by Niels Bohr in 1913, the Bohr model revolutionized our understanding of atomic structure. It departed from classical physics by positing that electrons orbit the nucleus only in specific, quantized energy levels or shells. Unlike classical physics predictions, these orbits are stable, and electrons do not radiate energy while orbiting in these defined paths.
Quantized Energy Levels: The Foundation of Atomic Stability
The concept of quantized energy levels is central to the Bohr model. This principle asserts that electrons can only occupy discrete energy states, much like steps on a ladder. Electrons cannot exist between these energy levels. Each energy level corresponds to a specific orbit around the nucleus. The energy of an electron is directly related to the size of its orbit.
Lower energy levels are closer to the nucleus, while higher energy levels are further away. These energy levels are often denoted by the principal quantum number n, where n = 1, 2, 3, and so on, representing the ground state and successively higher energy states.
Niels Bohr’s Groundbreaking Contribution
Niels Bohr’s genius lay in synthesizing classical and quantum ideas. He adapted Max Planck’s concept of quantization. This was previously applied to energy radiated by blackbodies, and boldly applied it to the structure of the atom.
Bohr’s model successfully explained the discrete spectral lines of hydrogen. This was a major triumph that established the model as a significant advancement in atomic theory. The model earned him the Nobel Prize in Physics in 1922.
Planck’s Constant: The Quantum of Action
Planck’s constant (h), a fundamental constant in quantum mechanics, plays a vital role in the Bohr model. It relates the energy of a photon to its frequency (E = hν), where E is energy, ν is frequency, and h is approximately 6.626 x 10^-34 joule-seconds.
In the context of the Bohr model, Planck’s constant governs the energy differences between electron energy levels. When an electron transitions from one energy level to another, it emits or absorbs energy in discrete packets, or quanta, that are proportional to Planck’s constant. This quantization of energy is what ultimately gives rise to the discrete lines observed in atomic emission spectra.
Before delving into the specifics of potassium’s spectral signature, it’s essential to revisit the Bohr model of the atom. While superseded by more sophisticated quantum mechanical models, the Bohr model provides an intuitive and accessible framework for understanding atomic emission, particularly when considering elements with simpler electronic structures.
With a foundational understanding of the Bohr model now established, we can apply its principles to unravel the intricacies of potassium’s atomic structure, setting the stage for understanding its unique emission spectrum.
Potassium’s Atomic Blueprint: Structure and Electron Configuration
Potassium (K), an alkali metal, holds atomic number 19, dictating its fundamental structure. The identity and behavior of any element are rooted in the arrangement and quantity of its constituent subatomic particles. Let’s break down the atomic blueprint of potassium, focusing on the number of protons, neutrons, and electrons and the subsequent electron configuration.
Defining Potassium’s Atomic Composition
The nucleus of a potassium atom invariably contains 19 protons. This number is its defining characteristic, differentiating it from all other elements. The number of protons dictates the element’s chemical identity and its position on the periodic table.
Neutrons, on the other hand, can vary, leading to the existence of isotopes. The most abundant isotope of potassium, Potassium-39, contains 20 neutrons (39 – 19 = 20). Other isotopes, like Potassium-40 and Potassium-41, exist with different numbers of neutrons.
In a neutral potassium atom, the number of electrons orbiting the nucleus equals the number of protons in the nucleus, resulting in a balanced charge. Therefore, a neutral potassium atom possesses 19 electrons.
Electron Configuration: The Arrangement of Potassium’s Electrons
The arrangement of these 19 electrons within the atom is defined by its electron configuration. Understanding this configuration is crucial for predicting potassium’s chemical behavior and, most importantly for our purposes, its emission spectrum. Electrons do not orbit the nucleus randomly; they occupy specific energy levels or shells, as described by the Bohr model, and subshells within those levels.
The electron configuration of potassium is 1s²2s²2p⁶3s²3p⁶4s¹. This notation reveals the distribution of electrons across different energy levels:
-
The first energy level (n=1) holds 2 electrons in the 1s subshell.
-
The second energy level (n=2) holds 8 electrons in the 2s (2 electrons) and 2p (6 electrons) subshells.
-
The third energy level (n=3) holds 8 electrons in the 3s (2 electrons) and 3p (6 electrons) subshells.
-
The fourth energy level (n=4) holds 1 electron in the 4s subshell.
The Significance of the Valence Electron
Notice that the outermost shell, the fourth energy level (n=4), contains only one electron in the 4s subshell. This outermost electron is known as the valence electron. It is this single valence electron that is primarily responsible for potassium’s characteristic chemical properties and its distinctive emission spectrum. It is the transitions of this electron that give rise to the observable spectral lines.
The relatively low energy required to remove this valence electron makes potassium highly reactive, readily losing it to form a positive ion (K+). This ease of ionization is also fundamental to understanding how potassium atoms absorb energy and subsequently emit light, leading to its characteristic emission spectrum.
A neutral potassium atom, therefore, possesses 19 electrons. Now that we understand potassium’s atomic structure, we can explore how these electrons orchestrate the element’s unique emission spectrum.
Decoding Potassium’s Emission Spectrum: A Dance of Electrons and Photons
The vibrant colors observed when potassium compounds are heated, the lilac flame test familiar to chemistry students, are direct manifestations of its emission spectrum. This spectrum, a unique fingerprint for potassium, arises from the orchestrated movement of its electrons, a delicate dance of absorption and emission.
Electron Excitation and the Creation of Light
At its core, an emission spectrum is generated through electron transitions within an atom. Under normal circumstances, electrons reside in the lowest possible energy states, also known as the ground state.
However, when energy is supplied to the atom – whether through heat, electricity, or radiation – electrons can absorb this energy and jump to higher energy levels, called excited states. These excited states are inherently unstable.
The electron will spontaneously return to a lower energy level, eventually reaching its ground state. This transition releases the excess energy in the form of a photon, a particle of light.
Wavelength and Energy: A Direct Relationship
The crucial aspect is that the energy of the emitted photon is directly proportional to the difference in energy between the initial (excited) state and the final (lower) state of the electron. This energy difference dictates the photon’s frequency, and consequently, its wavelength.
Because only specific, quantized energy levels are allowed within an atom (as dictated by the Bohr model, and more precisely by quantum mechanics), only photons with specific wavelengths can be emitted. These discrete wavelengths constitute the element’s unique emission spectrum.
For potassium, the most prominent emission lines fall within the visible spectrum, specifically in the violet-blue region, which is why potassium flames appear lilac.
The specific electron transitions that give rise to these lines involve the single valence electron in potassium’s outermost shell. Transitions from higher energy p orbitals to the s orbital give rise to intense spectral lines.
Spectroscopic Analysis: Unveiling the Spectral Fingerprint
The emission spectrum isn’t just a pretty display; it’s a powerful analytical tool. Spectroscopy techniques are employed to precisely measure the wavelengths and intensities of the emitted light, allowing scientists to identify and quantify the presence of potassium.
Flame photometry is a common analytical technique that leverages this principle. A sample containing potassium is introduced into a flame, and the emitted light is passed through a spectrometer. The intensity of the characteristic potassium emission lines is then measured, which is directly proportional to the concentration of potassium in the sample.
More advanced techniques, such as atomic emission spectroscopy (AES), utilize plasmas or other high-energy sources to excite the atoms, providing even greater sensitivity and enabling the detection of trace amounts of potassium.
By analyzing the emitted light, one can determine not only the presence but also the concentration of potassium in a wide range of samples, from soil and water to biological tissues and even distant stars. This highlights the importance of understanding the fundamental principles behind potassium’s emission spectrum.
The stage is now set to explore how these principles manifest in the unique spectral signature of potassium.
The Bohr Model in Action: Predicting Potassium’s Emission Lines
The beauty of the Bohr model lies in its ability to quantitatively predict the wavelengths of light emitted by an element, aligning remarkably well (at least for simpler atoms) with experimentally observed emission spectra. For potassium, this predictive power allows us to connect specific electron transitions to the characteristic lines seen in its spectrum.
Quantifying Energy Levels and Transitions
The Bohr model posits that electrons occupy discrete energy levels, often visualized as orbits around the nucleus. Each orbit corresponds to a specific energy value. When an electron transitions from a higher energy level (ni) to a lower one (nf), the energy difference (ΔE) is released as a photon.
This energy difference is directly related to the frequency (ν) and wavelength (λ) of the emitted light through the following equations:
ΔE = hν
ν = c/λ
Where:
- h is Planck’s constant (approximately 6.626 x 10-34 J·s)
- c is the speed of light (approximately 3.00 x 108 m/s)
By calculating the energy difference between specific energy levels in potassium, we can predict the frequency and wavelength of the emitted photons.
Prominent Emission Lines and Corresponding Transitions
Potassium exhibits several prominent emission lines, most notably in the visible and near-infrared regions of the spectrum. The most intense and well-known lines are a doublet in the red-violet region, appearing around 766.49 nm and 769.90 nm.
These lines are a fingerprint of potassium.
These prominent lines arise from transitions of the outermost electron (the 19th electron) from the 4p energy level to the 4s ground state.
Slight differences in energy within the 4p level (due to spin-orbit coupling, a phenomenon not fully explained by the Bohr model) result in the two closely spaced wavelengths. This is a key reason why there are often ‘doublets’ of colors observed.
Less intense lines are also observed at shorter wavelengths, corresponding to transitions from higher energy levels to lower ones. However, the 4p to 4s transitions dominate the emission spectrum due to their higher probability.
Frequency, Energy, and the Electromagnetic Spectrum
It’s crucial to understand the relationship between frequency, energy, and the position of emission lines within the electromagnetic spectrum. Higher frequency light corresponds to higher energy photons and shorter wavelengths. Conversely, lower frequency light corresponds to lower energy photons and longer wavelengths.
Potassium’s violet emission lines, therefore, are indicative of relatively high-energy transitions compared to, say, infrared emissions.
By carefully analyzing the frequencies (or wavelengths) of emitted light, we gain valuable insight into the energy level structure of the potassium atom and the dynamics of its electron transitions.
The spectral lines of potassium, meticulously predicted using the Bohr model, offer a compelling glimpse into the atom’s inner workings. This model, while incredibly useful for illustrating the basic principles of electron transitions and quantized energy levels, operates under significant simplifications.
Beyond Bohr: Acknowledging Limitations and Embracing Quantum Mechanics
The Bohr model, with its neat depiction of electrons orbiting the nucleus in fixed paths, provides an intuitive entry point into atomic physics. However, it’s crucial to recognize its inherent limitations when confronted with the complexities of multi-electron atoms and intricate spectral phenomena. The model’s inability to accurately predict the spectra of atoms beyond hydrogen underscores its incomplete nature.
The Bohr Model’s Shortcomings
One of the major shortcomings of the Bohr model is its assumption that electrons follow well-defined circular orbits. This contrasts sharply with the reality unveiled by quantum mechanics, which describes electrons as existing in probability distributions, or orbitals, rather than fixed trajectories. The model also fails to account for the fine structure and hyperfine structure observed in atomic spectra.
These finer details, arising from relativistic effects and nuclear spin interactions, are beyond the scope of the Bohr model’s explanatory power. Furthermore, the model provides no mechanism for calculating the transition probabilities between energy levels. It merely postulates that transitions occur, without offering a quantitative framework for predicting their likelihood.
The Quantum Leap: A More Accurate Atomic Picture
Quantum mechanics provides a far more sophisticated and accurate description of atomic structure and electron behavior. The Schrödinger equation, a cornerstone of quantum mechanics, replaces the Bohr model’s classical orbits with atomic orbitals, which are three-dimensional mathematical functions describing the probability of finding an electron in a particular region of space.
Atomic Orbitals and Electron Configuration
These orbitals are characterized by a set of quantum numbers (principal, azimuthal, magnetic, and spin) that dictate the energy, shape, and spatial orientation of the electron’s probability distribution.
Quantum mechanics incorporates wave-particle duality of electrons. It acknowledges electrons’ wave-like behavior.
Quantum Electrodynamics (QED) and Spectral Details
Advancements like Quantum Electrodynamics (QED) further refine our understanding, accounting for interactions between electrons and photons. These interactions are responsible for the subtle spectral details that the Bohr model cannot explain. QED treats electromagnetic force between electrons and photons, offering incredible spectral predictive accuracy.
By solving the Schrödinger equation for a particular atom, physicists can calculate the energy levels and transition probabilities with remarkable precision. This is key. This ability to accurately predict and explain atomic phenomena underscores the power and elegance of quantum mechanics. It also highlights the limitations of the Bohr model as a stepping stone to more advanced concepts.
Beyond the theoretical underpinnings of electron behavior, potassium’s distinct spectral signature finds extensive application in diverse analytical techniques and observational sciences. Its readily identifiable emission lines serve as a powerful tool for both quantitative analysis in terrestrial laboratories and qualitative assessments of celestial bodies light-years away.
Applications of Potassium’s Spectral Fingerprint: From Labs to the Cosmos
The unique emission spectrum of potassium isn’t merely a subject of academic interest. It has profound practical applications, ranging from routine laboratory analyses to groundbreaking discoveries in astrophysics.
Flame Photometry: Quantifying Potassium in the Lab
Flame photometry, also known as flame emission spectroscopy, leverages the principles of atomic emission to determine the concentration of certain elements, including potassium, in a sample.
This technique involves introducing a sample into a flame, which causes the potassium atoms to become excited. As these excited atoms return to their ground state, they emit photons of characteristic wavelengths.
The intensity of the emitted light at these specific wavelengths is directly proportional to the concentration of potassium in the sample. By comparing the intensity of the emitted light from the unknown sample to that of known standards, the concentration of potassium can be accurately determined.
Flame photometry is widely used in various fields, including:
- Agriculture (analyzing soil and fertilizer samples)
- Environmental science (monitoring water quality)
- Clinical chemistry (measuring potassium levels in blood and urine).
Its relative simplicity and cost-effectiveness make it a valuable tool for routine potassium analysis.
Potassium in the Cosmos: An Astrophysical Tracer
The distinct spectral lines of potassium also serve as a crucial tool for astronomers seeking to understand the composition and characteristics of distant stars, nebulae, and even exoplanetary atmospheres.
When light from these celestial objects passes through a spectroscope, the resulting spectrum reveals the presence of specific elements based on their unique emission or absorption lines.
The identification of potassium’s spectral lines in the light from a star, for instance, provides direct evidence of its presence within that star’s atmosphere.
The intensity and broadening of these lines can further reveal information about the star’s temperature, density, and velocity.
By analyzing the spectra of numerous stars, astronomers can map the distribution of potassium and other elements throughout the galaxy, gaining insights into stellar evolution, nucleosynthesis, and the chemical composition of the universe.
Moreover, the detection of potassium in the atmospheres of exoplanets, though challenging, can provide clues about their potential habitability and overall composition. It’s a valuable piece of evidence to help identify the environments in the vast universe where life could have the right conditions to potentially exist.
Potassium’s Emission: Bohr Model Explained – FAQs
Here are some frequently asked questions to help you better understand potassium’s emission spectrum and the Bohr model.
Why does potassium emit light at specific wavelengths?
Potassium emits light at specific wavelengths because its electrons can only exist at certain energy levels, as described by the Bohr model. When an electron transitions from a higher energy level to a lower one, it releases energy in the form of a photon with a specific wavelength corresponding to the energy difference.
How does the Bohr model explain potassium’s emission spectrum?
The Bohr model explains potassium’s emission spectrum by illustrating the allowed electron orbits around the nucleus. Each electron transition between these orbits results in the emission of light with a specific energy and wavelength, creating the distinct lines observed in potassium’s emission spectrum.
What happens to the electron during potassium’s emission?
During emission, an electron in potassium drops from a higher, excited energy level to a lower, more stable energy level. The energy difference between these levels is released as a photon, contributing to potassium’s emission spectrum and its bohr model showing the electron transitions.
Does every element have a unique emission spectrum like potassium?
Yes, every element has a unique emission spectrum. This is because each element has a different number of protons and electrons, resulting in distinct energy levels and electron transition possibilities. Hence, potassium’s emission spectrum and its bohr model showing the electron transitions are unique to potassium.
So, there you have it – a simplified look at potassium’s emission spectrum and its bohr model showing the electron transitions! Hopefully, it helped make things a little clearer. Go explore, and maybe you’ll even discover something new yourself!