Understanding the concept of symmetry is fundamental to grasping trigonometric functions, particularly when exploring what does it mean to say a trig function is even. At its core, evenness in functions, a property often visually demonstrated on a Cartesian plane, implies a specific type of symmetry about the y-axis. This symmetry reflects the relationship between inputs and outputs, a concept rigorously defined in mathematical analysis. Consider, for instance, how this property influences the behavior of functions like cosine; its inherent evenness distinguishes it from functions exhibiting other types of symmetries.
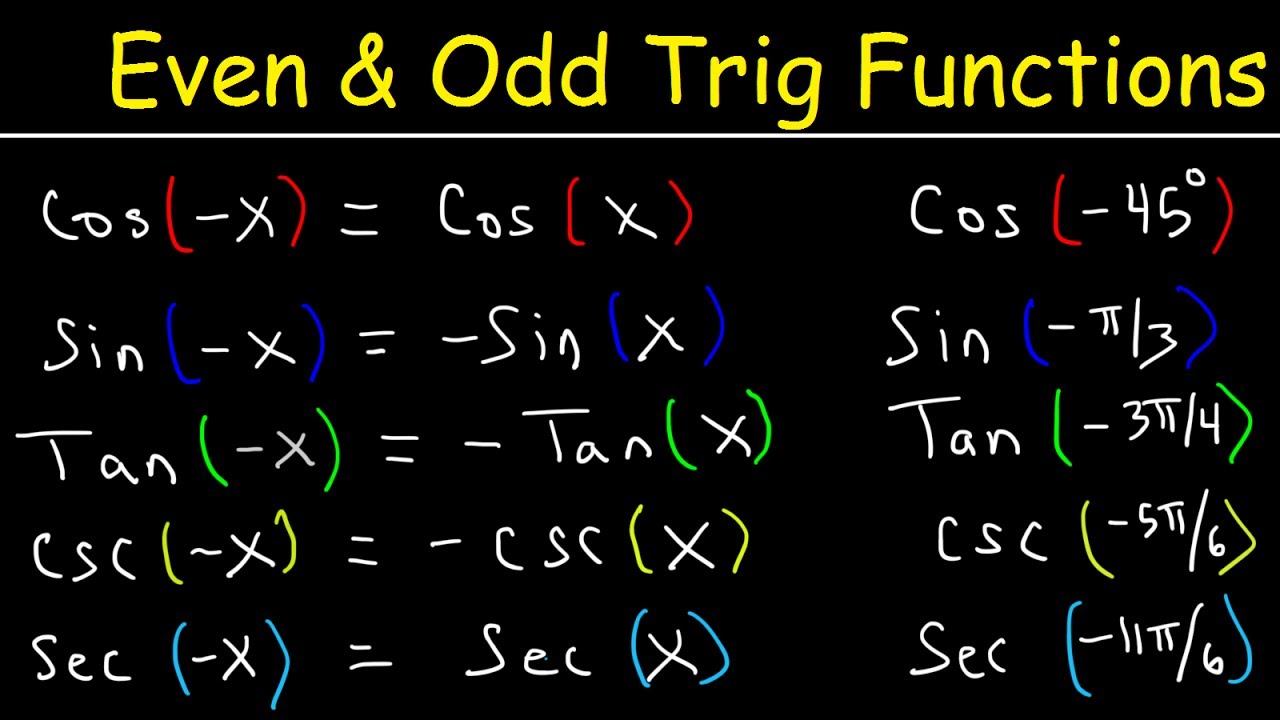
Image taken from the YouTube channel The Organic Chemistry Tutor , from the video titled Even and Odd Trigonometric Functions & Identities – Evaluating Sine, Cosine, & Tangent .
Unveiling the Mystery of Even Trigonometric Functions
Trigonometry, the branch of mathematics dealing with relationships between the sides and angles of triangles, is fundamental to various scientific and engineering disciplines. From calculating the trajectory of a projectile to modeling sound waves, trigonometry provides the tools necessary to understand and predict periodic phenomena. But have you ever stopped to wonder why the trigonometric functions don’t all behave the same way?
Why is it that some functions, like cosine, exhibit a unique property of symmetry, while others do not?
This article delves into the fascinating world of even trigonometric functions, specifically exploring what makes them "even." We will unravel the mystery behind this behavior by examining key concepts such as the definition of an even function in general, and how it applies specifically to the cosine and secant functions.
We will also explore the concept of symmetry, particularly as it relates to the y-axis, and how negative angles play a crucial role in understanding even functions. Finally, we will utilize the unit circle as a visual aid to solidify your understanding of this important concept. By the end of this exploration, you’ll gain a clear understanding of what it means for a trigonometric function to be even and why only certain functions possess this intriguing property.
Understanding Even Functions: The Foundation
Before diving into the specifics of even trigonometric functions, it’s crucial to establish a firm understanding of what constitutes an even function in mathematics generally. This concept forms the bedrock for understanding the behavior of cosine and secant.
Defining Even Functions
An even function is defined mathematically by a specific property: for any input x, the function produces the same output as it does for its negative counterpart, -x. This can be succinctly expressed by the equation:
f(x) = f(-x)
This equation is the key to identifying and working with even functions.
Symmetry About the Y-Axis
The mathematical definition translates directly into a visual characteristic: symmetry about the y-axis. If you were to graph an even function, the left side of the graph (for negative x values) would be a mirror image of the right side (for positive x values), with the y-axis acting as the mirror. This symmetry is a hallmark of even functions.
Non-Trigonometric Examples
To illustrate this concept with more familiar examples, consider the functions f(x) = x² and g(x) = x⁴.
Let’s test f(x) = x²:
f(-x) = (-x)² = x² = f(x)
Similarly, for g(x) = x⁴:
g(-x) = (-x)⁴ = x⁴ = g(x)
Both functions satisfy the f(x) = f(-x) criterion. Therefore, they are even functions, and their graphs exhibit symmetry about the y-axis.
Testing for Even Functions Algebraically
To formally determine whether a given function is even, you need to perform an algebraic test. This involves substituting -x for x in the function’s equation and then simplifying the expression.
If the simplified expression is identical to the original function, then the function is even. If, instead, you obtain the negative of the original function, then the function is odd. If the result is neither identical to the original function nor its negative, then the function is neither even nor odd.
For example, let’s test the function h(x) = x³ + x:
h(-x) = (-x)³ + (-x) = -x³ – x = -(x³ + x) = -h(x)
Since h(-x) = -h(x), this function is an odd function, not an even function, demonstrating a crucial distinction. A strong understanding of the algebraic test for even functions is imperative before delving into even trigonometric functions.
Cosine: The Prime Example of an Even Trig Function
Having established the foundation of even functions, we can now turn our attention to the cosine function, the quintessential example of an even trigonometric function. Understanding why cosine exhibits this property provides a powerful illustration of the broader concept of evenness in mathematics.
Unveiling the Cosine Function
The cosine function, denoted as cos(x), is a fundamental trigonometric function that relates an angle in a right triangle to the ratio of the adjacent side to the hypotenuse. In the context of the unit circle, cos(x) represents the x-coordinate of the point on the circle corresponding to the angle x.
The graph of the cosine function is a smooth, wave-like curve that oscillates between -1 and 1. This graphical representation is crucial for visualizing its even symmetry.
The Core Property: cos(x) = cos(-x)
The defining characteristic of the cosine function’s evenness lies in the equation cos(x) = cos(-x). This equation states that the cosine of an angle is equal to the cosine of its negative counterpart.
But what does this mean geometrically, and why is it true?
The Unit Circle Perspective
The unit circle provides an elegant explanation. In the unit circle, angles are measured counterclockwise from the positive x-axis. A negative angle, -x, is measured clockwise from the same axis.
Consider an angle x and its negative counterpart -x on the unit circle. The x-coordinate of the point corresponding to angle x is cos(x), and the x-coordinate of the point corresponding to angle -x is cos(-x).
Because of the symmetry of the circle, these two points will have the same x-coordinate. This demonstrates visually why cos(x) = cos(-x).
 is the same for both positive and negative angles of the same magnitude, illustrating the even property of the cosine function.</em></p>
<h3><span class=) Y-Axis Symmetry
Y-Axis Symmetry
The property cos(x) = cos(-x) translates directly into y-axis symmetry in the graph of the cosine function. If you were to fold the graph along the y-axis, the left and right sides would perfectly overlap.
This symmetry is a visual confirmation of the cosine function’s even nature. The graph serves as a powerful tool for understanding and remembering this essential property.
Why Cosine is Even: A Unit Circle Perspective
As we saw, the equation cos(x) = cos(-x) is the key to understanding the even nature of the cosine function. But to truly grasp this concept, we need to delve deeper into the unit circle and explore the geometric relationships between angles and their negative counterparts. Let’s unravel the symmetry within.
Angles and Their Negatives on the Unit Circle
Imagine an angle x radiating counterclockwise from the positive x-axis within the unit circle. Now, picture its negative counterpart, -x, extending clockwise the same distance from the same axis. These angles are essentially mirror images of each other with respect to the x-axis.
This symmetry is crucial. Because they are mirror images in the x-axis, their projection down to the x-axis is equal, i.e. have the same x coordinate. Since cosine represents the x-coordinate on the unit circle, cos(x) and cos(-x) land on the same x-value.
Cosine and the Adjacent Side: A Right Triangle View
To solidify this understanding, let’s bring in a right triangle.
Consider the right triangle formed by dropping a perpendicular line from the point on the unit circle (corresponding to angle x) to the x-axis. The cosine of angle x is, by definition, the length of the adjacent side divided by the hypotenuse (which is 1 in the unit circle). Hence, the adjacent side’s length is the cosine value.
Now, consider the right triangle formed by the negative angle -x. Notice something remarkable: the adjacent side of angle x is equal to the adjacent side of angle -x. Since the hypotenuse is also the same (radius of the unit circle), it directly follows that:
cos(x) = adjacent/hypotenuse = adjacent/1 = adjacent = cos(-x)
Therefore, the cosine of an angle and its negative are inherently equal due to this shared adjacent side length. This elegantly demonstrates why the cosine function maintains its even property.
Secant: Cosine’s Even Twin
Having established the even nature of the cosine function through the lens of the unit circle and its inherent symmetry, we can now readily extend this understanding to another crucial trigonometric function: the secant.
The secant function, often abbreviated as sec(x), is defined as the reciprocal of the cosine function. This relationship is fundamental:
sec(x) = 1 / cos(x)
The Reciprocal Relationship
Because secant and cosine are reciprocals, the properties of one directly influence the other. If cosine exhibits even symmetry, its reciprocal must follow suit.
Evenness of Secant: A Direct Consequence
The mathematical proof is straightforward. We know that cos(x) = cos(-x) because cosine is an even function. Therefore:
sec(x) = 1 / cos(x)
sec(-x) = 1 / cos(-x)
Since cos(x) = cos(-x), it logically follows that:
1 / cos(x) = 1 / cos(-x)
Thus, sec(x) = sec(-x)
This confirms that the secant function is also an even function.
Visualizing Secant’s Symmetry
The graph of the secant function visually reinforces this concept. Like the cosine function, the secant function exhibits symmetry about the y-axis. This means that if you were to fold the graph along the y-axis, the two halves would perfectly overlap.
The secant graph has vertical asymptotes where the cosine function equals zero, as division by zero is undefined. The "U" shapes open upwards or downwards depending on the sign of the cosine function within that interval. However, overall, the secant graph mirrors itself across the y-axis, a defining characteristic of even functions.
Understanding the secant function as the reciprocal of the even cosine function provides a quick and intuitive grasp of its own even nature, highlighting the interconnectedness of trigonometric relationships.
The section to be written is:
<li>
<p><strong>Visualizing Even Symmetry: Cosine vs. Secant</strong></p>
<p>Display the graphs of the cosine and secant functions side-by-side to visually emphasize the concept of y-axis symmetry. Briefly contrast with the graphs of odd trigonometric functions (sine, tangent) and their different symmetries (or lack thereof).</p>
<ul>
<li>Show the <strong>Graphs of Trigonometric Functions</strong> (Cosine and Secant) side-by-side to visually reinforce the concept of y-axis <strong>Symmetry</strong>.</li>
<li>Contrast with examples of odd trig functions (Sine, Tangent) and their symmetry.</li>
</ul>
</li>
Visualizing Even Symmetry: Cosine and Secant
Having established both algebraically and through the unit circle that cosine and secant functions are even, a visual comparison of their graphs powerfully reinforces this concept.
By placing the graphs side-by-side, the characteristic symmetry about the y-axis becomes immediately apparent. This visual confirmation solidifies the understanding of what it means for a function to be even.
Side-by-Side Comparison: Cosine and Secant Graphs
The cosine function undulates smoothly, its peaks and troughs mirroring each other perfectly across the y-axis. For every point (x, cos(x)) on the graph, the point (-x, cos(x)) also exists.
The secant function, being the reciprocal of the cosine, inherits this symmetry.
While its graph is characterized by vertical asymptotes wherever cos(x) = 0, the overall shape still demonstrates even symmetry. The "U" shaped sections of the graph are mirrored across the y-axis, creating a visually striking illustration of the sec(x) = sec(-x) relationship.
Contrasting with Odd Functions: Sine and Tangent
To further appreciate the even symmetry of cosine and secant, it’s insightful to contrast them with odd trigonometric functions such as sine and tangent.
Odd functions exhibit a different type of symmetry – symmetry about the origin. This means that f(-x) = -f(x).
Sine Function: Symmetry About the Origin
The sine function’s graph clearly demonstrates this origin symmetry. As x increases, sin(x) increases from 0 to 1, then back to 0. On the other side, as x decreases from 0, sin(x) decreases to -1.
If you rotate the sine function 180 degrees about the origin, the graph remains unchanged, showcasing its odd symmetry.
Tangent Function: Asymptotic Oddity
The tangent function, like sine, is also an odd function. Its graph, punctuated by vertical asymptotes, extends infinitely in both positive and negative directions.
While visually distinct from the sine wave, it still exhibits symmetry about the origin, further highlighting the difference between odd and even functions.
By contrasting the graphs of even (cosine, secant) and odd (sine, tangent) trigonometric functions, we gain a deeper appreciation for the concept of symmetry in mathematics and how it manifests in different functions. The y-axis symmetry of cosine and secant provides a clear visual marker of their even nature, distinguishing them from functions with other types of symmetries.
Having established both algebraically and through the unit circle that cosine and secant functions are even, a visual comparison of their graphs powerfully reinforces this concept. By placing the graphs side-by-side, the characteristic symmetry about the y-axis becomes immediately apparent. This visual confirmation solidifies the understanding of what it means for a function to be even.
Practical Implications and Uses of Even Functions
The property of evenness in functions, particularly trigonometric functions like cosine and secant, isn’t merely a theoretical curiosity. Understanding and recognizing this characteristic can lead to significant simplifications in calculations and problem-solving, particularly in applied fields. Let’s explore some practical implications and applications.
Simplifying Calculations
One of the most immediate benefits of recognizing an even function is its ability to simplify calculations involving negative inputs. Since f(x) = f(-x) for an even function, you can often replace a negative input with its positive counterpart without altering the result. This can be especially useful when dealing with complex equations or scenarios where working with positive values is more convenient.
Applications in Physics and Engineering
Even trigonometric functions frequently arise in various branches of physics and engineering. Their symmetrical properties make them indispensable in modeling phenomena that exhibit similar symmetries. Here are a few specific examples:
-
Wave phenomena: Cosine functions are fundamental in describing wave motion, such as sound waves and electromagnetic waves. Due to their even nature, cosine functions can represent waves propagating in either direction equally well, simplifying the analysis of wave interference and superposition.
-
Alternating current (AC) circuits: The voltage and current in AC circuits are often modeled using sinusoidal functions (sine and cosine). The cosine function’s even property is leveraged when analyzing power dissipation and energy storage in these circuits, as the sign of the current or voltage doesn’t affect the overall power calculation.
-
Structural mechanics: In structural analysis, cosine functions are used to describe stress and strain distributions in symmetrical structures. The even symmetry simplifies the analysis of bending moments and shear forces.
-
Optics: Cosine functions are used to model light waves. Their even property is important for analyzing interference patterns and diffraction phenomena.
Example Calculation: Cosine in Action
Consider a scenario in physics where you need to calculate the horizontal displacement of a pendulum bob at a specific time. The displacement can be modeled using the equation:
x(t) = A cos(ωt)
**
where:
- x(t) is the horizontal displacement at time t.
- A is the amplitude of the swing.
- ω is the angular frequency.
Suppose you need to find the displacement at t = -π/ω. Using the even property of the cosine function:
x(-π/ω) = A cos(ω (-π/ω)) = A cos(-π)**
Since cos(-π) = cos(π), you can directly substitute:
x(-π/ω) = A cos(π) = A (-1) = -A
Therefore, the displacement is -A. This example demonstrates how recognizing the even nature of the cosine function simplifies the calculation by allowing you to work with the equivalent positive angle. This principle can be extended to significantly more complex calculations in real-world applications, saving time and reducing the risk of error.
FAQs: Even Trig Functions Explained
Still have questions about even trig functions? Here are some common questions to help clarify the concept.
What exactly does it mean to say a trig function is even?
When we say a trig function is even, it means that the function’s value is the same for both an angle and its negative. Mathematically, this is expressed as f(-x) = f(x). Think of it as the function having symmetry about the y-axis.
Which trig functions are even?
Only two trig functions are even: cosine (cos x) and secant (sec x). Their values remain unchanged when the angle’s sign is flipped, meaning cos(-x) = cos(x) and sec(-x) = sec(x).
Why are cosine and secant even functions while sine and tangent are not?
Cosine and secant are even because of the way they are defined on the unit circle. Cosine corresponds to the x-coordinate, and secant is the reciprocal of cosine. Changing the sign of the angle reflects the point across the x-axis, leaving the x-coordinate (and thus cosine and secant) unchanged. Sine and tangent, which relate to the y-coordinate, do change sign upon reflection.
How can knowing a trig function is even help me solve problems?
Knowing that a trig function is even simplifies calculations. If you know cos(30°), you automatically know cos(-30°) is the same value. This symmetry can significantly speed up solving trigonometric equations and simplifying expressions.
Alright, hopefully, you now have a solid handle on what does it mean to say a trig function is even. Go forth and conquer those trig problems!